Event JSON
{
"id": "1db6e706048a62e7f8e24a8adb4b090ae594f036e301b0a1d4e353b7f399f7d2",
"pubkey": "9a6a1a8eefd0b53d7e0c966ab35bd904151246f03b1be98fa0d2d0eeb4940320",
"created_at": 1742924481,
"kind": 1,
"tags": [
[
"proxy",
"https://mathstodon.xyz/@johncarlosbaez/114224298810149620",
"web"
],
[
"e",
"7e243db284346c5afe51994c3e116ac2c74f68708e503080eb250ae63502f64a",
"",
"root",
"9a6a1a8eefd0b53d7e0c966ab35bd904151246f03b1be98fa0d2d0eeb4940320"
],
[
"p",
"9a6a1a8eefd0b53d7e0c966ab35bd904151246f03b1be98fa0d2d0eeb4940320"
],
[
"imeta",
"url https://media.mathstodon.xyz/media_attachments/files/114/224/263/953/454/058/original/c586f14d107b1182.jpg",
"m image/jpeg"
],
[
"p",
"920836d45c3d9b8a98392001ea5d3f9a7cce05db058db85a385c159076d99618"
],
[
"proxy",
"https://mathstodon.xyz/users/johncarlosbaez/statuses/114224298810149620",
"activitypub"
],
[
"L",
"pink.momostr"
],
[
"l",
"pink.momostr.activitypub:https://mathstodon.xyz/users/johncarlosbaez/statuses/114224298810149620",
"pink.momostr"
],
[
"-"
]
],
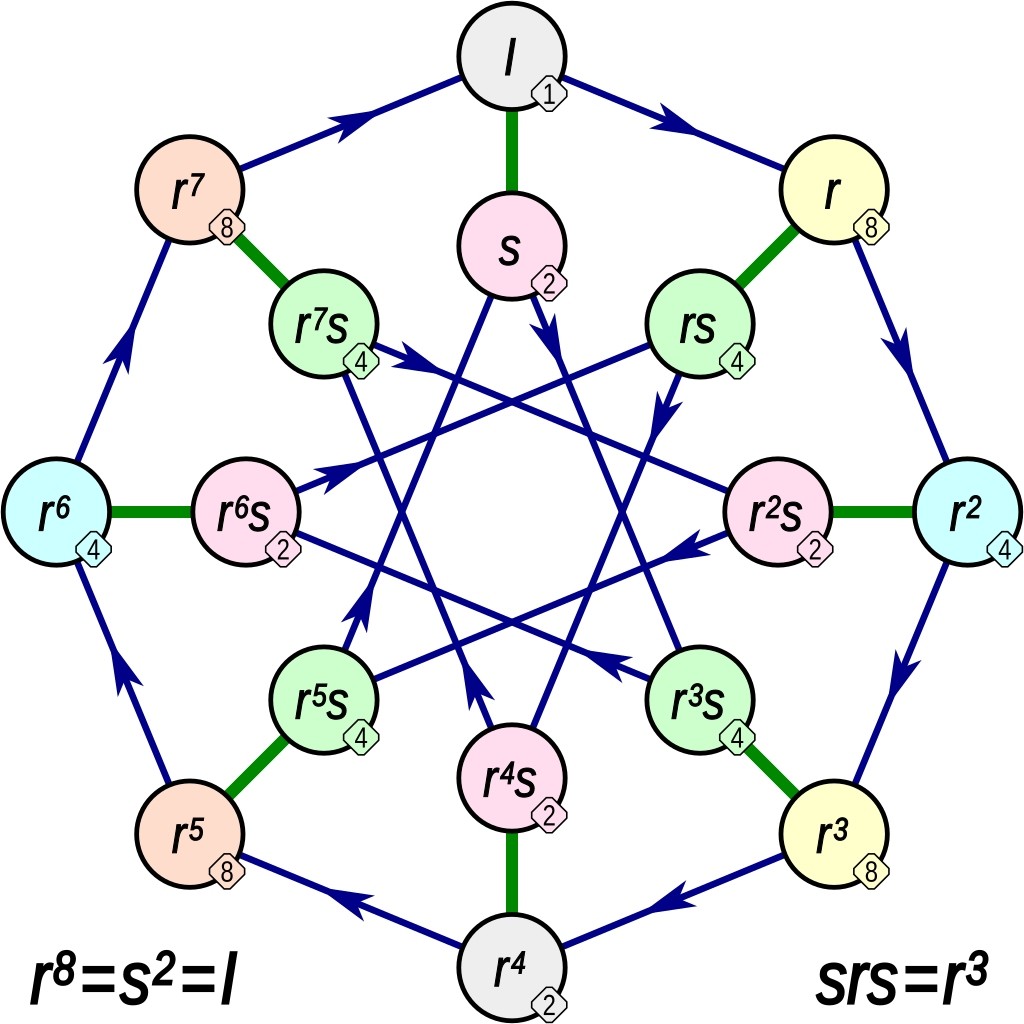
"content": "Now I'll the same stuff like a mathematician: we saw that the dihedral group with 16 elements, also called 𝐷₁₆, has a presentation with generators 𝑟,𝑠 and relations\n\n𝑟⁸ = 𝑠² = (𝑟𝑠)² = 𝐼,\n\nWe also saw its Cayley diagram, labeling each group element by its order.\n\nQuicker, but fewer people will understand! \n\nNow for something a bit less known. The group we just saw has an evil twin, another group with 16 elements, called the 'quasidihedral group'. Only one of the relations is different: now we have \n\n𝑠𝑟𝑠 = 𝑟³ \n\nThis makes the Cayley diagram look like an 8-pointed star inside an octagon!\n\nI heard about this group from nostr:npub1jgyrd4zu8kdc4xpeyqq75hflnf7vupwmqkxmsk3cts2eqakejcvqc8rkt6, and I instantly looked it up on Wikipedia, where they have these nice pictures:\n\nhttps://en.wikipedia.org/wiki/Quasidihedral_group\n\nIn fact ost finite groups have a size that's a power of two! So there are a *lot* of different groups with 16 elements - namely, 14 of them. So, if you were stuck on a desert island, you could have fun figuring out what they all are, and drawing the Cayley diagrams of all 14. In fact if the world keeps going to hell, I might go to a desert island and do just that.\n\n(2/2)\nhttps://media.mathstodon.xyz/media_attachments/files/114/224/263/953/454/058/original/c586f14d107b1182.jpg\n",
"sig": "483d5eb1cb866d9b65fca5ec9d096acf7a20a78f9a1de8c168653d7180a63633297efc53e625562eccab1fae44cf664a511bf80c66b05771792053c2cfe94c99"
}