John Carlos Baez on Nostr: Take a regular octagon, like an American stop sign. It has a bunch of symmetries... ...

Take a regular octagon, like an American stop sign. It has a bunch of symmetries... and this is a picture of all its symmetries!

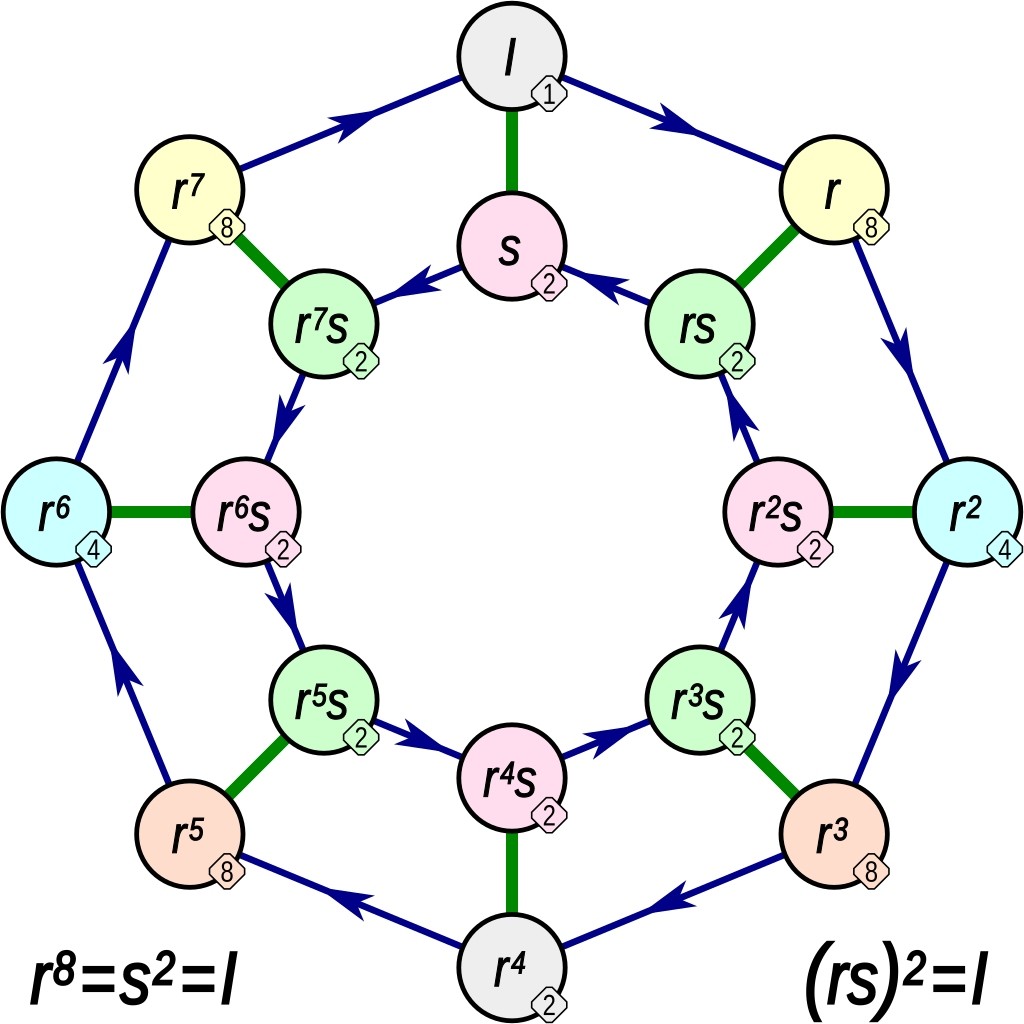
You can do nothing to it: that operation is called 𝐼. You can rotate it an eighth of a turn clockwise: that's called 𝑟. You can do that twice: this is called 𝑟². And so on, up to 𝑟⁷. When you rotate your octagon an eighth of a turn 8 times it's back to where it started, so

𝑟⁸ = 𝐼

But you can also flip the sign over, say along the vertical axis. Let's call that operation 𝑠. If you flip it over twice it's back to where it started, so

𝑠² = 𝐼

There's one other equation that's less obvious. Rotate it an eighth of a turn clockwise, flip it over along the vertical axis, and the rotate it an eighth of a turn clockwise again. This is the same as just flipping it over: the two rotations cancel out! So

𝑟𝑠𝑟 = 𝑠

(The picture states this equation another way: 𝑟𝑠𝑟𝑠 = 𝐼, or (𝑟𝑠)²=𝐼 for short. It's equivalent.)

The picture shows all the different operations you can get by doing 𝑟 and 𝑠. There are only 16, namely these:

𝐼, 𝑟, 𝑟², 𝑟³, 𝑟⁴, 𝑟⁵, 𝑟⁶, 𝑟⁷

and the 8 operations you get by rotating any amount and then flipping:

𝑠, 𝑟𝑠, 𝑟²𝑠, 𝑟³𝑠, 𝑟⁴𝑠, 𝑟⁵𝑠, 𝑟⁶𝑠, 𝑟⁷𝑠

In the picture, the arrows show what happens when you do another rotation 𝑟: for example there's an arrow from 𝑟⁶ to 𝑟⁷, or less obviously from 𝑟𝑠 to 𝑠 because

𝑟𝑠𝑟 = 𝑠

The green lines show what happens when you do 𝑠.

Finally, the little numbers say how many times you have to do an operation to get back to where you started! For example, if you rotate an octagon a quarter turn that's 𝑟². If you do this 4 times you get back where you started, so the number next to 𝑟² is 4.

(1/2)