twofish on Nostr: In stalking the wild pendulum, information density is talked about, e.g. But also in ...

In stalking the wild pendulum, information density is talked about, e.g.



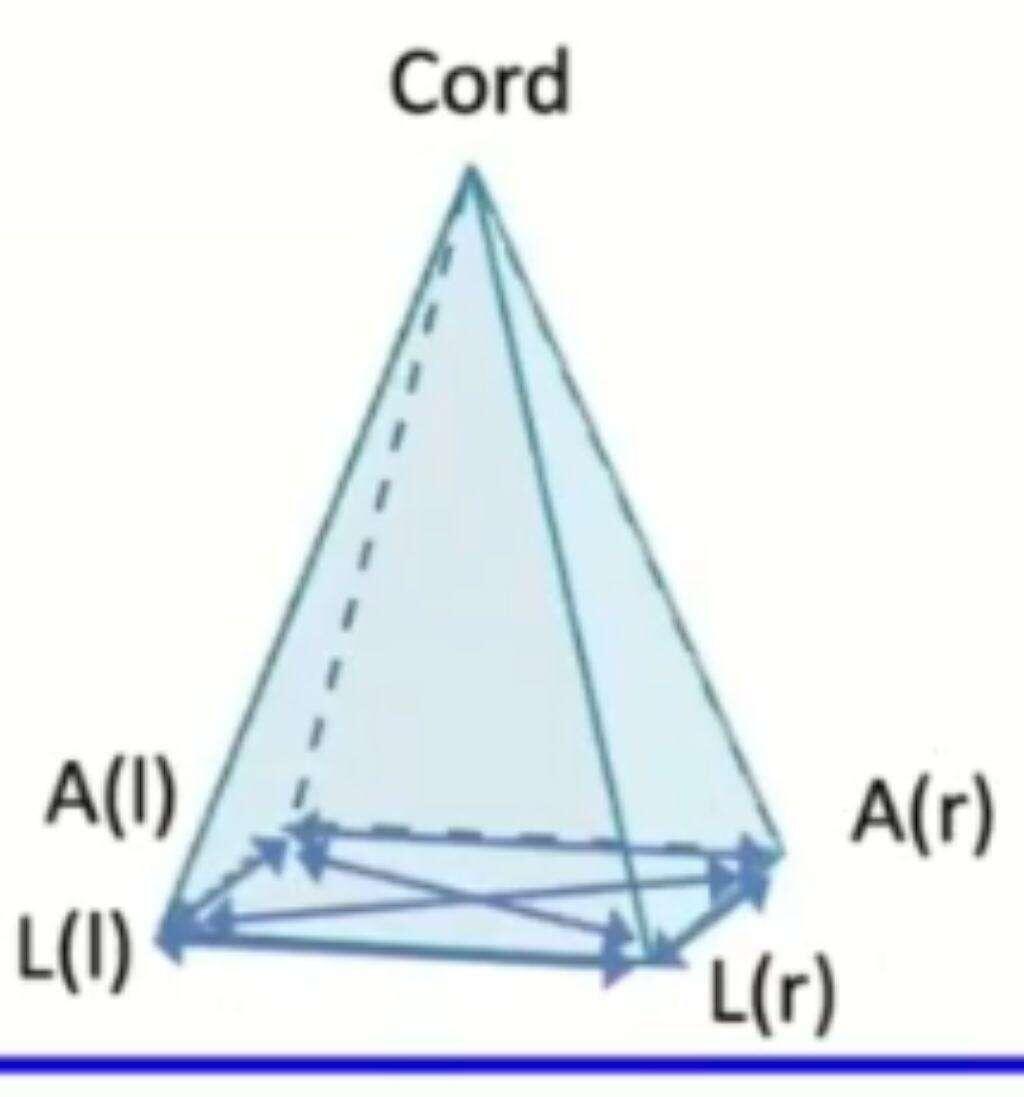
But also in other parts of the book.


I just have this perspective based on my background in data science that maps the spirit to these sets of components in latent space, which are basically these components built from eigenvectors sorted by their variance or information density.

The way this works mathematically is well explained here, where the author starts out with:

Imagine a big family dinner where everybody starts asking you about PCA. First, you explain it to your great-grandmother; then to your grandmother; then to your mother; then to your spouse; finally, to your daughter (a mathematician). Each time the next person is less of a layman. Here is how the conversation might go.

https://stats.stackexchange.com/questions/2691/making-sense-of-principal-component-analysis-eigenvectors-eigenvalues#140579

And then finally in the video above the talks about correlation vs causality, which talks about movements in latent space, which is to say, given a set of components, say you had the pca algorithm generate 5 components. Now the set is sorted by information density, and say each one is represented as a slider. As you move the slider from left to right, each slider represents a move in latent space that changes the output and/or outcome, in the form of a transformation.

When applied to a dataset of faces for example, the first slider might be the hair style, the second my be their smile, third might be their eye expression, the last one might not do anything noticeable because of its low information density meaning that it has no real impact on the output and/or outcome.

Why does this matter?
In the second video he talks about moving your x and nothing happens on y, which is the output and/or outcome. Let's add some detail to that.
We observed a doll move, and we are trying to understand how it works based on our observations. We haven't built a map yet of what makes the doll move (the latent space).
Let's say we want a smile. We've seen an example of smiling so we know it's possible, but we can't find the dimension that applies to that. We try changing various input vectors, but nothing happens to the output and/or outcome that produces a smile. So we begin mapping out this black box, trying to change different inputs to see what happens on the output.

We write down what we learn, e.g.



We still don't understand the coord.

Then, somehow, someway, we get that ah hah moment. We discover the cord.



It was in another dimension, a higher dimension.

This is what it feels like to me learning about your work. You have found the cord!