Dan Piponi on Nostr: The group law for an a elliptic curve over ℂ makes it a differentiable manifold ...
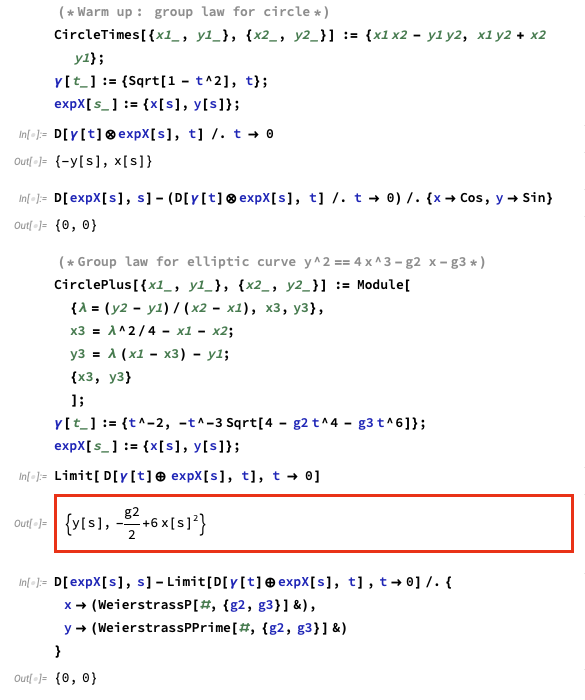
The group law for an a elliptic curve over ℂ makes it a differentiable manifold with a differentiable group structure so it's a Lie group with a Lie algebra and an exponential map. This exponential map is in fact the Weierstrass ℘-function and the corresponding "logarithm" is the Abel-Jacobi map. For some reason no book I've read on elliptic curves mentions this fact.
I've been meaning to do this calculation for over 30 years and I kept putting it off - but I finally got around to deriving the differential equation for the exponential map and was actually kinda excited to see it's precisely he equation satisfied by ℘.
I don't know why this isn't in all the text books. You can literally just read off the Abel-Jacobi map which is now well motivated rather than being this thing you can concoct and whose properties you discover after the fact.
(Maybe at some point I'll write up in more detail what's going on here.)
Published at
2025-04-08 15:14:59Event JSON
{
"id": "c6ccfb086a072897337ee2ae051998184377345ccc0fd1722b7d9b78a3f09c2a",
"pubkey": "3422fcbc32f333fb2d3481b2e981258af8a0b571869cbfe93c42962410e232ef",
"created_at": 1744125299,
"kind": 1,
"tags": [
[
"imeta",
"url https://media.mathstodon.xyz/media_attachments/files/114/302/986/586/462/149/original/5bcdab22a19b11dc.png",
"m image/png",
"dim 585x700",
"blurhash U5Ss5001%M?bk=f6RkaeWCafayoficR*fkt7"
],
[
"proxy",
"https://mathstodon.xyz/users/dpiponi/statuses/114302995635252142",
"activitypub"
],
[
"client",
"Mostr",
"31990:6be38f8c63df7dbf84db7ec4a6e6fbbd8d19dca3b980efad18585c46f04b26f9:mostr",
"wss://relay.mostr.pub"
]
],
"content": "The group law for an a elliptic curve over ℂ makes it a differentiable manifold with a differentiable group structure so it's a Lie group with a Lie algebra and an exponential map. This exponential map is in fact the Weierstrass ℘-function and the corresponding \"logarithm\" is the Abel-Jacobi map. For some reason no book I've read on elliptic curves mentions this fact.\n\nI've been meaning to do this calculation for over 30 years and I kept putting it off - but I finally got around to deriving the differential equation for the exponential map and was actually kinda excited to see it's precisely he equation satisfied by ℘.\n\nI don't know why this isn't in all the text books. You can literally just read off the Abel-Jacobi map which is now well motivated rather than being this thing you can concoct and whose properties you discover after the fact.\n\n(Maybe at some point I'll write up in more detail what's going on here.)\n\nhttps://media.mathstodon.xyz/media_attachments/files/114/302/986/586/462/149/original/5bcdab22a19b11dc.png",
"sig": "0aad68906b26b1dfddaa21632657d87f4ca078d838644a393374af27157d6a1a15eb8edf0305fd1fff1270e51e4df12f4c1fd00df5f9ee1c6ba130b28d986d42"
}
