But on a surface of constant negative curvature, like this tractroid, no such obstacle exists, and every non-meridian geodesic on the tractroid has 2 inflection pts (black).
Greg Egan on Nostr: No smooth curve that lies on a sphere can contain an inflection point (a point where ...
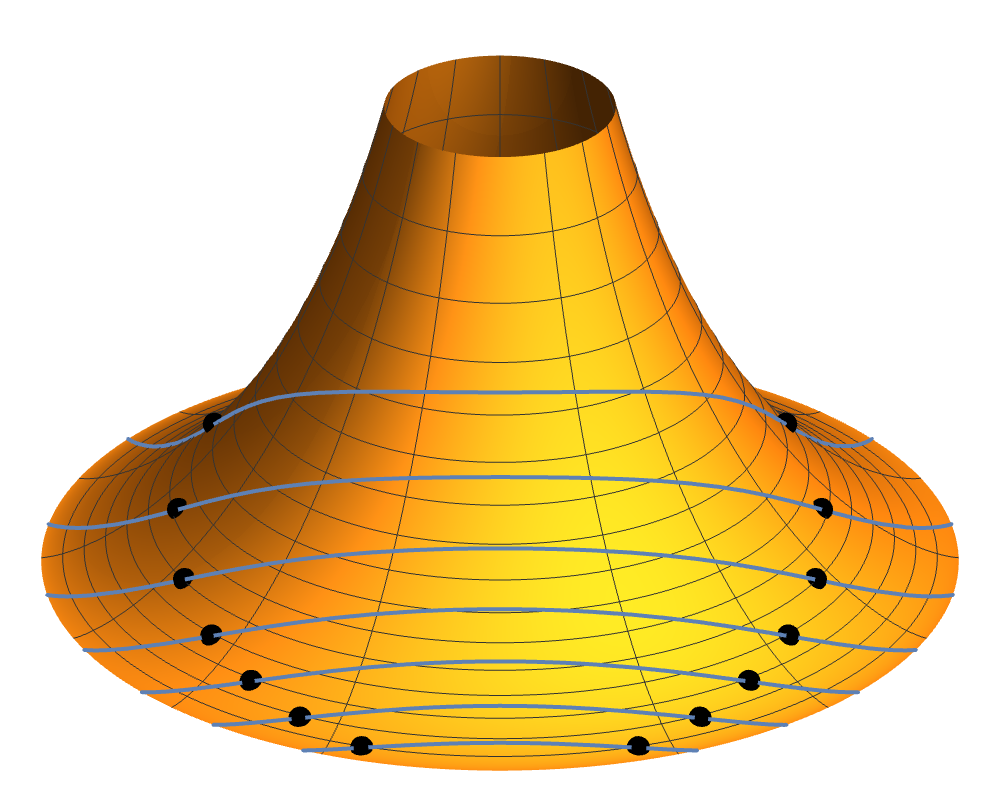
No smooth curve that lies on a sphere can contain an inflection point (a point where the curvature is zero).
But on a surface of constant negative curvature, like this tractroid, no such obstacle exists, and every non-meridian geodesic on the tractroid has 2 inflection pts (black).
But on a surface of constant negative curvature, like this tractroid, no such obstacle exists, and every non-meridian geodesic on the tractroid has 2 inflection pts (black).