Event JSON
{
"id": "39ae44effd1f66199255d88503df589058ea51de1618114a087800f2f1ddb0dc",
"pubkey": "ec4c0474085a36db6717feba02f56f9b360dba572291fe9bb3fa3ae819f98b04",
"created_at": 1743677895,
"kind": 1,
"tags": [
[
"p",
"b4c50e1bc1d7c4e1372d0c767c4705509f070b0f3109447d90cd0eb34a992896",
"wss://relay.mostr.pub"
],
[
"p",
"5fb5d869121f82243d7d155f9a521b94b28dc8e5e37c87d35d065a57de1ec127",
"wss://relay.mostr.pub"
],
[
"p",
"0037e9f1404aa866c76ed1358206ac5387eb2d3589361a3802af0f260bda26d7",
"wss://relay.mostr.pub"
],
[
"p",
"f7346eb283902ada9d21c109a93e83128d9f87d8fcfe70ad819b3bf2ad9bce16",
"wss://relay.mostr.pub"
],
[
"e",
"47ad563069ea641b828d2e0e231b0a9f8e1be0a420f7db371a16a9599b691de8",
"wss://relay.mostr.pub",
"reply"
],
[
"imeta",
"url https://media.mathstodon.xyz/media_attachments/files/114/273/632/953/793/240/original/e898c8dadb604a19.jpg",
"m image/jpeg",
"dim 918x1224",
"blurhash UcH2cx%2DNV?xtWVaekCITfkxbj[o#j]WBWB"
],
[
"proxy",
"https://mathstodon.xyz/users/GerardWestendorp/statuses/114273674537047033",
"activitypub"
]
],
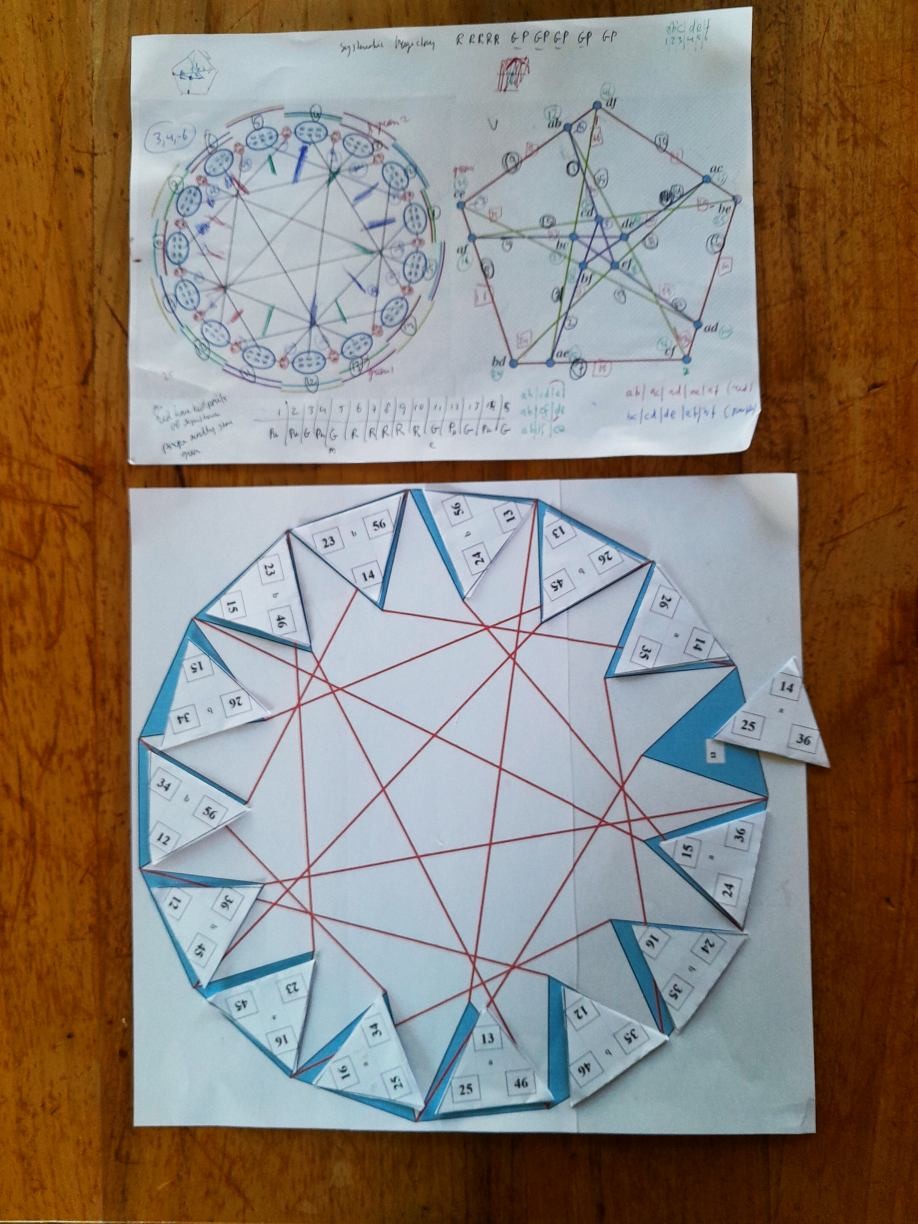
"content": "nostr:nprofile1qy2hwumn8ghj7un9d3shjtnddaehgu3wwp6kyqpqknzsux7p6lzwzdedp3m8c3c92z0swzc0xyy5glvse58txj5e9ztqaufa4k nostr:nprofile1qy2hwumn8ghj7un9d3shjtnddaehgu3wwp6kyqpqt76as6gjr7pzg0taz40e55smjjegmj89ud7g056aqed90hs7cynsacyu7x \nNow for the relationship with the Tutte Coxeter graph. I've printed the \"synthemes\" (triplets of duads) on triangles, with the mirror image on the back. So I can \"Triomino\" a labeling of the Tutte Coxeter graph. I've convinced myself that laying down 2 adjacent synthemes conpletely fixes the labeling. Makes sense, there are 720 ways of doing that, and 720 inner automorphisms of the graph.\n\nhttps://media.mathstodon.xyz/media_attachments/files/114/273/632/953/793/240/original/e898c8dadb604a19.jpg",
"sig": "92aa439950702af8adad6e05e5d90f161d4b25e9e8811318c52d4422ca52f29c650f05bf12af14e8715c58310df03011c8cbbbb1e9bf6e97265e8282f9ca8673"
}