Greg Egan on Nostr: The volume of a ball of radius r in n dimensions is B(n,r) = π^{n/2}/Γ(n/2+1) r^n ...

The volume of a ball of radius r in n dimensions is

B(n,r) = π^{n/2}/Γ(n/2+1) r^n

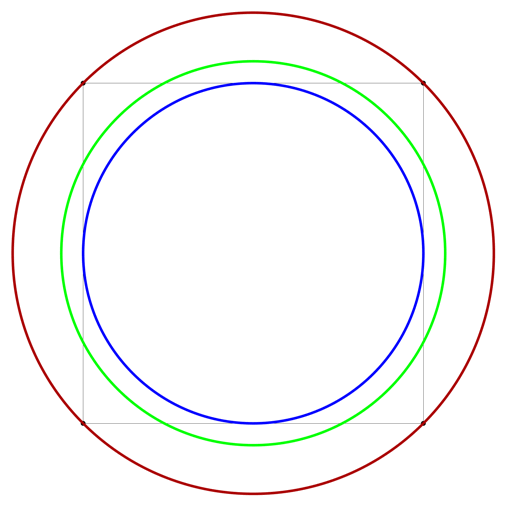
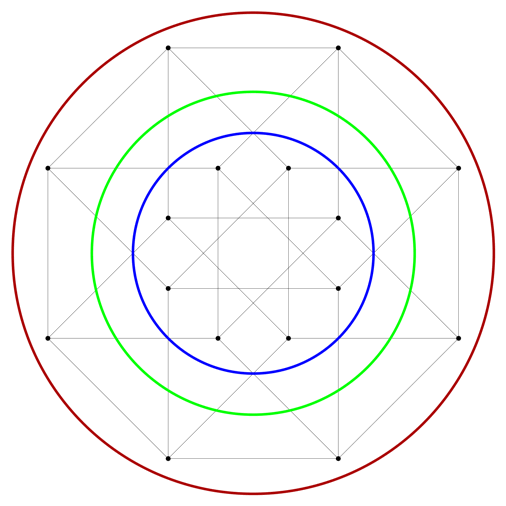
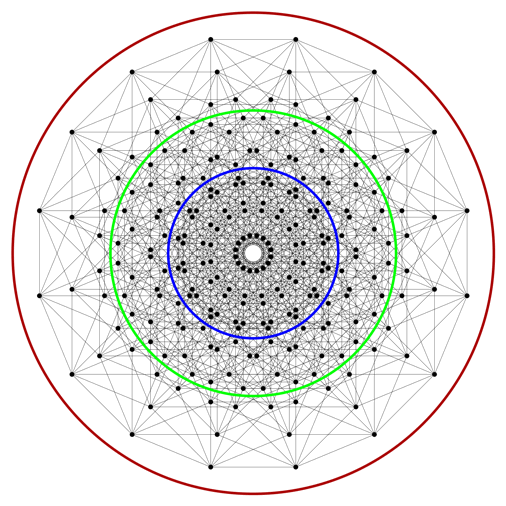
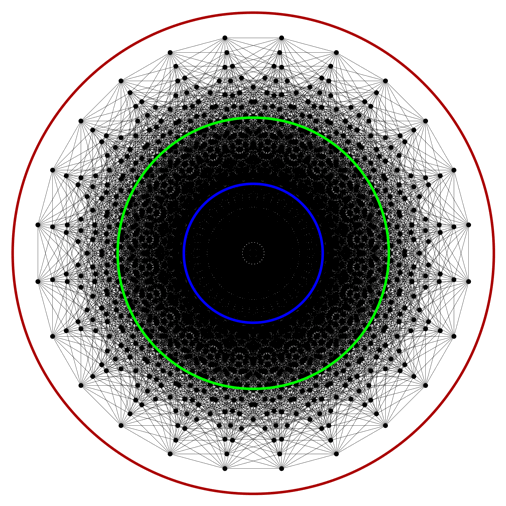
If you look at the volumes of the balls (blue circles) inscribed inside hypercubes with edge length 1 and volume 1, they go to zero as n gets larger:

lim n→∞ B(n,½) = 0

If you look at the volumes of the balls (red circles) that circumscribe each hypercube (of diagonal √n), they go to infinity:

lim n→∞ B(n,½√n) = ∞

But what if you always choose the radius of an n-ball so that its volume is exactly 1 (green circles)?

r₁(n) = Γ(n/2+1)^{1/n} / √π

This gives us B(n,r₁(n)) = 1

It turns out that:

lim n→∞ (r₁(n) - √[n/(2eπ)]) = 0

In other words, r₁(n) is asymptotic to a multiple of √n, so it approaches a fixed ratio with the length of the diagonal of the hypercube with the same volume.