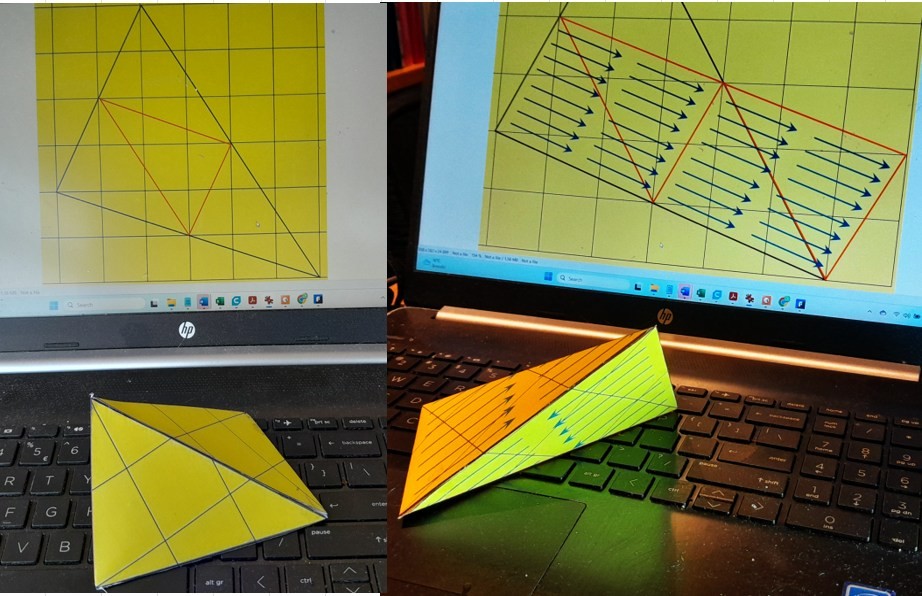
Gerard Westendorp on Nostr: I am still playing around a bit with the "Thurston Polyhedra" following the recent ...

I am still playing around a bit with the "Thurston Polyhedra" following the recent discussion started by nprofile1qy2hwumn8ghj7un9d3shjtnddaehgu3wwp6kyqpqknzsux7p6lzwzdedp3m8c3c92z0swzc0xyy5glvse58txj5e9ztqaufa4k (nprofile…fa4k), I made a tetrahedron on a square grid. I was surprised that the tetrahedron was tiled exactly by 14 squares. Thinking about it further, I realized that a tetrahedron made from congruent triangles admits sets of parallel geodesic loops of the same length. On the sphere, this is impossible: Latitude lines are not geodesics, and longitude lines intersect at the poles.