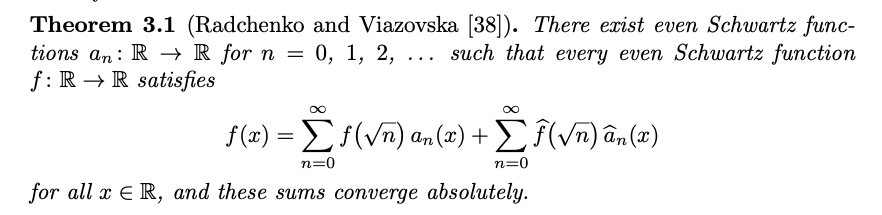Dan Piponi on Nostr: This is a really nice expository paper by Henry Cohn "From sphere packing to Fourier ...
This is a really nice expository paper by Henry Cohn "From sphere packing to Fourier interpolation":
https://www.arxiv.org/abs/2407.14999It gives a surprisingly readable account of work by Fields Medalist Maryna Viazovska.
I want to mention one particular theorem that's easy to state and has nice connections to signal processing.
Suppose you have some function f (with some technical side conditions) with Fourier transform F. If we know that if F is zero outside of a certain interval centred on zero then Nyquist-Shannon tells us we can reconstruct f perfectly knowing only ...f(-2), f(-1), 0, f(1), f(2), ... . All of our audio processing, and much of our image processing, is built on this assumption. In addition, given any choice of values of f(i) we can reconstruct a corresponding f.
But here's a weird and wonderful variant: Suppose f is even (satisfying certain technical conditions about decaying fast enough at infinity). Now also suppose we know f(0), f(1), f(√2), f(√3), ... and also we know F(0), F(1), F(√2), F(√3), ..., then in this case we can still perfectly reproduce f. We can also reconstruct a suitable f given any choice of f(√i) and F(√i) except for one linear constraint coming from the Poisson summation formula: we need f(0)+2f(1)+2f(2)+... = F(0)+2F(1)+2F(2)+... . This looks like something that should have been known classically but it's a 21st century result due to Radchenko and Viazovska. The proof makes use of my favourite functions, the theta functions.
There's an amazing connection between Fourier transforms and sphere packing and an n-dimensional variant of this theorem allows us to prove that E₈ and the Leech lattice are optimal lattice packings of spheres in 8 and 24 dimensions.
Published at
2024-08-01 02:44:44Event JSON
{
"id": "9b0eb62d6313808bf5e680efdd16e820addeaf3f798c2ef51b27ad844400e5e0",
"pubkey": "378fb8535da3c841fdebd0966e5a16f3d21d4e988b925e471f2d8fdf2345d2e9",
"created_at": 1722480284,
"kind": 1,
"tags": [
[
"proxy",
"https://mathstodon.xyz/@dpiponi/112884467893030693",
"web"
],
[
"imeta",
"url https://media.mathstodon.xyz/media_attachments/files/112/884/419/866/427/114/original/b160126d48a5cd5f.png",
"m image/png"
],
[
"proxy",
"https://mathstodon.xyz/users/dpiponi/statuses/112884467893030693",
"activitypub"
],
[
"L",
"pink.momostr"
],
[
"l",
"pink.momostr.activitypub:https://mathstodon.xyz/users/dpiponi/statuses/112884467893030693",
"pink.momostr"
],
[
"-"
]
],
"content": "This is a really nice expository paper by Henry Cohn \"From sphere packing to Fourier interpolation\":\n\nhttps://www.arxiv.org/abs/2407.14999\n\nIt gives a surprisingly readable account of work by Fields Medalist Maryna Viazovska.\n\nI want to mention one particular theorem that's easy to state and has nice connections to signal processing.\n\nSuppose you have some function f (with some technical side conditions) with Fourier transform F. If we know that if F is zero outside of a certain interval centred on zero then Nyquist-Shannon tells us we can reconstruct f perfectly knowing only ...f(-2), f(-1), 0, f(1), f(2), ... . All of our audio processing, and much of our image processing, is built on this assumption. In addition, given any choice of values of f(i) we can reconstruct a corresponding f.\n\nBut here's a weird and wonderful variant: Suppose f is even (satisfying certain technical conditions about decaying fast enough at infinity). Now also suppose we know f(0), f(1), f(√2), f(√3), ... and also we know F(0), F(1), F(√2), F(√3), ..., then in this case we can still perfectly reproduce f. We can also reconstruct a suitable f given any choice of f(√i) and F(√i) except for one linear constraint coming from the Poisson summation formula: we need f(0)+2f(1)+2f(2)+... = F(0)+2F(1)+2F(2)+... . This looks like something that should have been known classically but it's a 21st century result due to Radchenko and Viazovska. The proof makes use of my favourite functions, the theta functions.\n\nThere's an amazing connection between Fourier transforms and sphere packing and an n-dimensional variant of this theorem allows us to prove that E₈ and the Leech lattice are optimal lattice packings of spheres in 8 and 24 dimensions.\nhttps://media.mathstodon.xyz/media_attachments/files/112/884/419/866/427/114/original/b160126d48a5cd5f.png\n",
"sig": "c95e604e1054b040a8193f1071a493326f7d703576f6bc928eb18e4d8279e1bec4dc32d9926f2f77fa168210be2f216bac23a3f9581f6c47ccb7a0fa82ea3377"
}