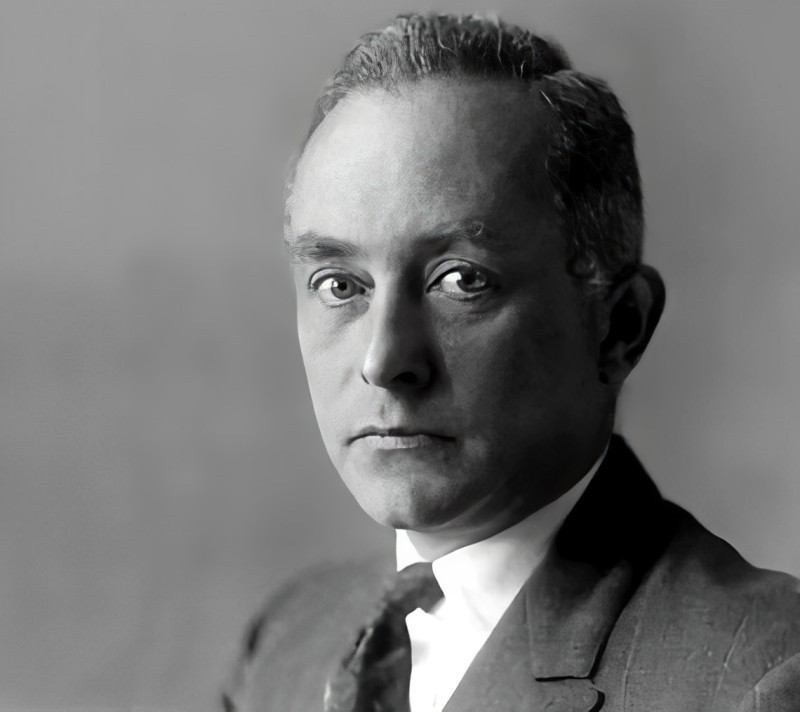Event JSON
{
"id": "79c9e3f878de97bd5df3bbad5730b5ef43c6170c600a0cedbc831e31d5b6f4f8",
"pubkey": "ce6cad7d0619fb4c94c45f2f0ef0d33aa5a22ecde2bc6cf00cac0551ad907694",
"created_at": 1733898023,
"kind": 1,
"tags": [
[
"t",
"maths"
],
[
"t",
"math"
],
[
"t",
"physics"
],
[
"t",
"wavefunction"
],
[
"t",
"quantummechanics"
],
[
"t",
"bornrule"
],
[
"t",
"maxborn"
],
[
"t",
"onthisday"
],
[
"imeta",
"url https://media.mathstodon.xyz/media_attachments/files/113/632/737/766/499/437/original/d4dd4fe7e29c13de.jpg",
"m image/jpeg",
"dim 800x712",
"blurhash UEE{kN~qIU9Fxuxu%MD%%MWBM{-;RjWBxuWB"
],
[
"proxy",
"https://mathstodon.xyz/users/dmm/statuses/113632740861840264",
"activitypub"
]
],
"content": "Born #onthisday in 1882, Max Born was one of the fundamental figures in the development of quantum mechanics. He was a mathematician, theoretical physicist and Nobel laureate.\n\nAmong the many mind-boggling things about quantum mechanics is Born's interpretation of the wave function ψ, known as the Born Rule [1]. According to the Born rule, if the wave function of the particle has the value ψ at some point x, then the probability of finding the particle between between x and x+dx is\n \n P(x ≤ x ≤ x+dx) = |ψ|² dx\n\nwhere |ψ|² is the probability density function for the particle's location.\n\n[Image credit: https://en.wikipedia.org/wiki/Max_Born]\n\nReferences\n------------\n[1] \"Born rule\", https://en.wikipedia.org/wiki/Born_rule\n\n#maxborn #bornrule #quantummechanics #wavefunction #physics #math #maths\n\nhttps://media.mathstodon.xyz/media_attachments/files/113/632/737/766/499/437/original/d4dd4fe7e29c13de.jpg",
"sig": "d379f78ba5ef8f41c7798b9513d23b032082b37c640a180119747943ea88f6919775fc7d965e36c0d66bec4035badd46aad3059f043a8972660204075cc36ead"
}