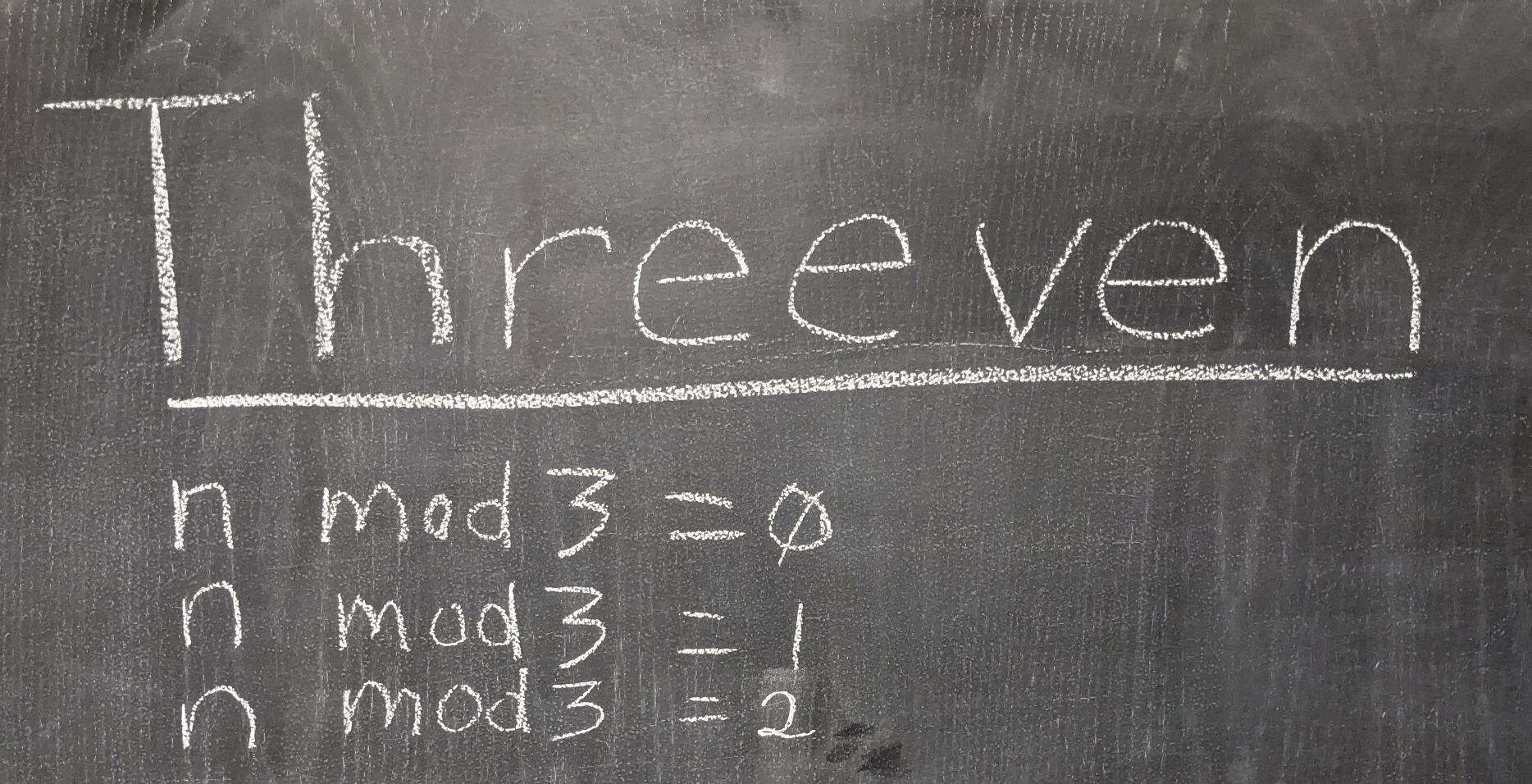We spend too much time enthralled by even numbers. We can instantly tell if a number is even or odd and often have preferences in the matter. In grade school we memorize rules like
- An even plus an even is an even
- An odd plus an odd is an even
- An even plus an odd is and odd
And so forth to rules of multiplication. But this magical quality of numbers really just means evenly divisible by 2. What is so special about 2? Shouldn’t we just as well care if a number is divisible by 3?
So I am introducing threeven numbers as all numbers divisible by 3.
0, 3, 6, 9, 12, 15, …
are all threeven numbers. But what about numbers that aren’t divisible by 3? Numbers that are not divisible 2 are called odd so I guess throdd?
There is, however, a slight problem. There seem to be more throdd numbers than threeven numbers.
1, 2, 4, 5, 7, 8, 10, 11, 13, 14, …
To solve that we need to think about what an odd number is. If an even number is some number n times 2 or 2n then odd numbers are 2n + 1
This gives a nice way to think about threeven numbers as well. Every threeven is 3n and a throdd is 3n + 1 and we need to introduce throdder numbers as 3n + 2. There isn’t any reason that there should only be two types of numbers. So instead of numbers that are divisible by 2 and numbers that aren’t, we have numbers that are divisible by 3, numbers that are 1 greater than a multiple of three and numbers that are 2 greater than a multiple of three.
To recap
- Threeven = 3n
- Throdd = 3n + 1
- Throdder = 3n + 2
Now for handy rules of thumb.
- A threeven plus a threeven is a threeven
- A threeven plus a throdd is a throdd
- A threeven plus a throdder is a throdder
- A throdd plus a throdd is a throdder
- A throdd plus a throdder is a threeven
- A throdder plus a throdder is a throdd
And, for multiplication
- A threeven times a threeven is a threeven
- A threeven times a throdd is a threeven
- A threeven times a throdder is a threeven
- A throdd times a throdd is a throdd
- A throdd times a throdder is a throdder
- A throdder times a throdder is a throdd
This is just modular arithmetic and the same can be done for any integer n
m mod n = 0
Means m is an nven and there will be n - 1 varieties of nodd
Threeven, however, is the most fun to say and makes the point nicely, there is no need to carry it further.
Note: it appears that I am not the first to have discovered threeven numbers. And now you are stuck knowing about them as well.