Wiki ＞
delta interaction

This article presents a theoretical framework for understanding how sensory experience and possibly qualia develop through the convolution of basic interactions. Rather than treating sensory experience as emergent from or separate from physical interactions, this theory proposes that experience is identical with specific patterns of convolved delta interactions across frequency domains. = Delta Interaction: Core Concept and Formalization

Figure 1. A demonstration of how binary interaction, and responses to interaction result in a continuous experience. The variance in responses is a result from tuning parameters for decay, temporal coherence : In black, we have an approximate delta response to the opposite extreme, a response with strong temporal coherence and a slow decay.

Introduction

The delta interaction is the fundamental, most basic unit of meaning and interaction.

Fundamental Axioms

Delta interactions are the primitive units of meaning and interaction.
Each delta interaction triggers a response in the system.

Mathematical Formalization

Delta Interaction δ(x, t)

Properties

Localized in space and time
Can vary in amplitude
Triggers a response in the system
Domain = {0} (strictly local, point-like)

Formalization

δ(x, t) = A · δ(x - x₀) · δ(t - t₀)

Where: * A is the input amplitude * x₀ is the position of interaction * t₀ is the time of interaction

d(x) = {1  if interaction present at x
0  if no interaction at x}

Response to Delta Interaction

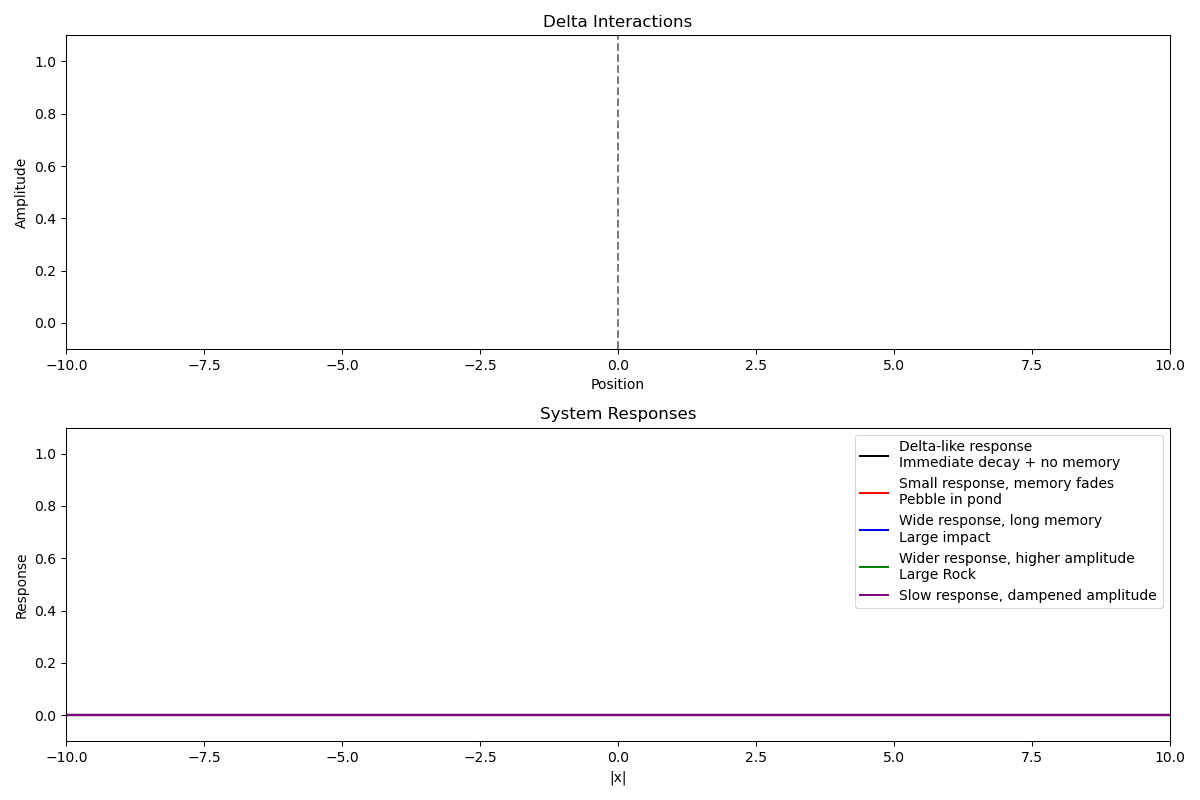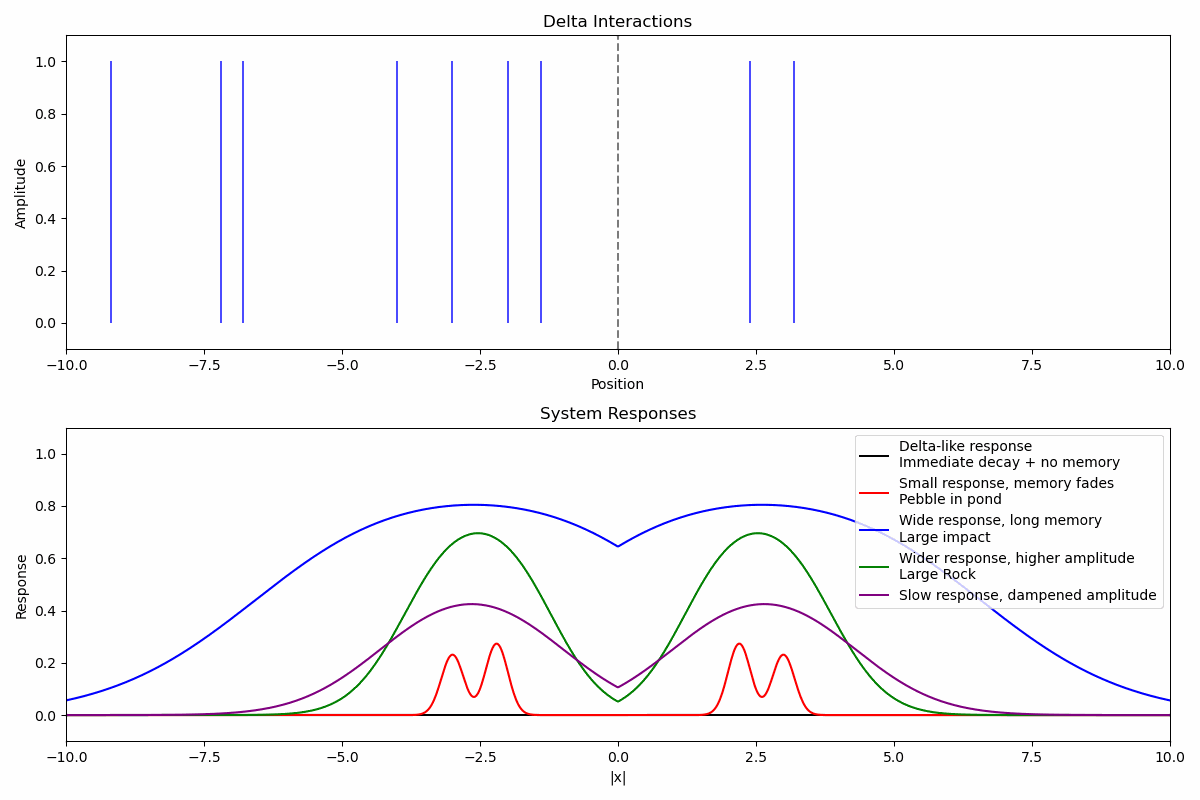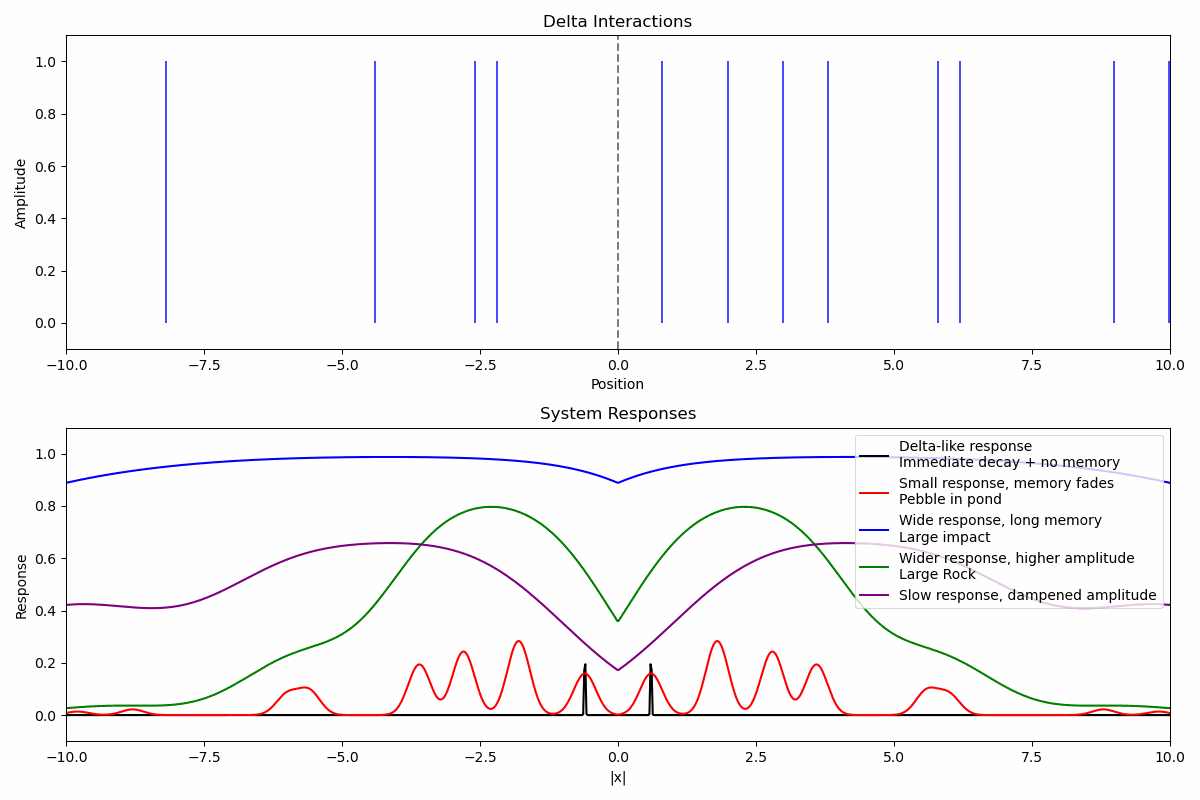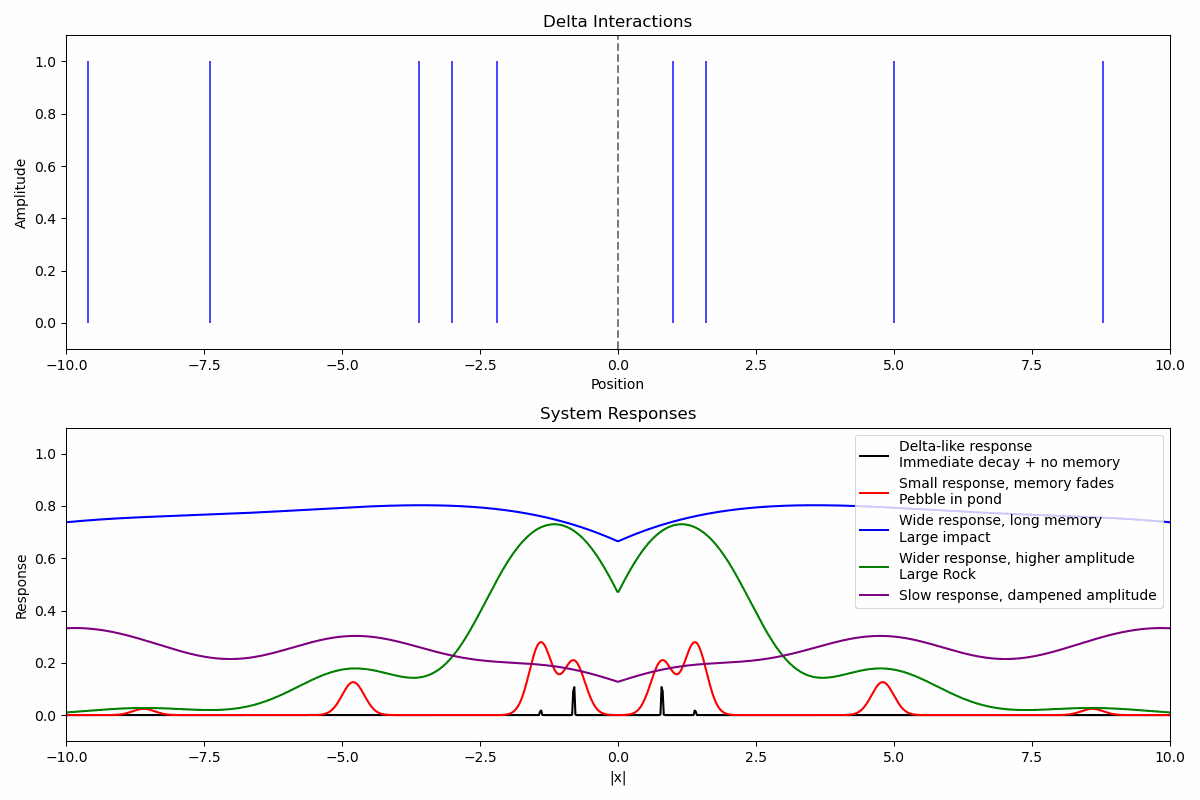
While the delta interaction itself is instantaneous and localized, it triggers a response in the system through a deformation from its initial state. The level of this deformation is how much the system has been perturbed, and how long the perturbation stays is a form of memory. This response can be modeled as a function R(x, t).

Response Function R(x, t)

R(x, t) = A₀ · e⁻ᵗ/τ · e⁻⟨(x - vt)²/(2σ²)⟩ · (1 - e⁻ʳᵗ)

Where: * A₀ is the response amplitude (related to input amplitude A) * τ is the temporal decay parameter (how quickly the response decays) * σ is the response width (spatial coherence of the response, i.e. how spread out it is) * v is the propagation velocity of the response (how fast the response spreads in space) * r is the rise rate of the response (how quickly the response reaches its peak)

Key Parameters of Delta Interactions

Input Amplitude (A)

Represents the strength or intensity of the interaction
Directly influences the magnitude of the system’s response

Position (x₀) and Time (t₀)

Define the exact location and moment of the interaction
Critical for understanding the spatiotemporal dynamics of the system === Decay Time (τ)
Given enough time, without any interaction, all systems will return to their initial, most entropic state.

Delta Interactions in Different Systems

Simple Systems

Delta interactions occur at a single point in space and time
No extension beyond immediate contact
Interaction measure: [source] m(s) = d(s)

Complex Systems

Interaction measure: [source] m(s) = ∫₀∞ P(s,t)dt where P(s,t) is the probability density of interactions

Interaction Patterns

Delta interactions create deformations in localized areas of the system which may propagate through temporally and spatially. Responses are dependent on the tuning of the system to the inputs. Multiple delta interactions with multiple types of systems responses combine to form complex patterns of interaction. The deformation from these patterns is how the system is able to hold on to meaning.

Basic Interaction Pattern

Pattern(x, t) = Σᵢ Aᵢ · δ(x - xᵢ, t - tᵢ)

Where: * Aᵢ represents the strength of each individual interaction * xᵢ, tᵢ represent the position and timing of each interaction

Relationship to Broader Framework

Delta interactions form the foundation of the Theory of Semiotic Interaction. They are the building blocks from which more complex structures, such as Cascading Semiotic Chains (CSCs), are constructed.

Wiki ＞delta interaction